Step-By-Step Examples > Example 8: Brick Patch Test

Problem Description

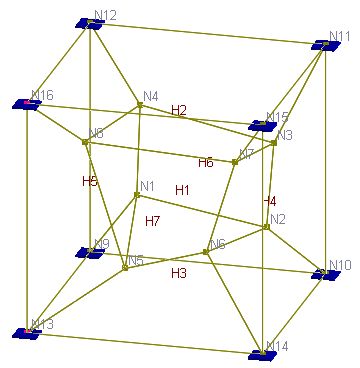
This is a patch test for a unit cube [Ref. 4 pp3-20]. The cube is modeled with 7 eight-node brick elements. Nodal coordinates, element connectivity and boundary conditions are given in the following tables. Boundary conditions are given as forced displacements. No additional loads are prescribed.

Material: E = 1.e6 psi; ν = 0.25

Find stresses for each element.

Example 8 Brick Patch Test1

Nodal coordinates (inch)

Node	X	Y	Z
1	0.249	0.342	0.192
2	0.826	0.288	0.288
3	0.85	0.649	0.263
4	0.273	0.75	0.23
5	0.32	0.186	0.643
6	0.677	0.305	0.683
7	0.788	0.693	0.644
8	0.165	0.745	0.702
9	0	0	0
10	1	0	0
11	1	1	0
12	0	1	0
13	0	0	1
14	1	0	1
15	1	1	1
16	0	1	1

Displacement field

u = 0.001 * (2x + y + z) / 2

v = 0.001 * (x + 2y + z) / 2

w = 0.001 * (x + y + 2z) / 2

Forced displacements (inch) on boundary

NODE	Dx	Dy	Dz
9	0	0	0
10	0.001	0.0005	0.0005
11	0.0015	0.0015	0.001
12	0.0005	0.001	0.0005
13	0.0005	0.0005	0.001
14	0.0015	0.001	0.0015
15	0.002	0.002	0.002
16	0.001	0.0015	0.0015

All strains are constant. For example

Element Connectivity

Element	Node1	Node2	Node3	Node4	Node5	Node6	Node7	Node8
1	1	2	3	4	5	6	7	8
2	4	3	11	12	8	7	15	16
3	9	10	2	1	13	14	6	5
4	2	10	11	3	6	14	15	7
5	9	1	4	12	13	5	8	16
6	9	10	11	12	1	2	3	4
7	5	6	7	8	13	14	15	16

Suggested Modeling Steps

▪Set proper units from Settings and Tools > Units & Precisions.

▪Input the nodal coordinates by Tables > Nodes.

▪Modify the default material by Tables > Materials.

▪Input the bricks by Tables > Bricks. Use the default material (=1).

▪Input the boundary conditions by Tables > Supports. Enter the support flag “111000” for each support. Enter the forced displacements according to the table above.

▪Set the analysis options by Analysis > Analysis Options. Choose the model type “3D Brick”.

Results

The comparison of stresses (psi) between the program and the referenced results is excellent. Each stress component is uniform in all seven elements.

	Sxx	Syy	Szz	Sxy	Syz	Sxz
ENERCALC 3D	1999.982	1999.982	1999.982	399.999	399.999	399.999
[Ref. 4]	2000	2000	2000	400	400	400

Comments

The brick element passes the patch test. Therefore, “the results for any problem solved with the element will converge toward the correct solution as the elements are subdivided.” [Ref. 4] The tiny differences in stresses are due to the penalty approach employed in support enforcement.