Navigation:  Step-By-Step Examples > Example 11: Frequencies of Cantilever Beam

Problem Description

Analyze the vibration frequencies for the following cantilever beam (L = 6m) under its own weight.

 

Material properties: E = 20600 KN/cm^2, ν = 0.3, weight density = 7850 Kgf/m^3

 

Section properties: Ix = 4079.07 cm^4, Ax = 53.1612 cm^2, Ay = Az = 0

 

The beam is optionally subjected to a compressive horizontal tip load of P = 500 KN

Analyze the beam for the following two cases:

a). Find the lowest 3 frequencies without the effect of axial load

b). Find the lowest 3 frequencies with the effect of axial load

 

 

Suggested Modeling Steps

▪Set proper units from Settings and Tools > Units & Precisions.

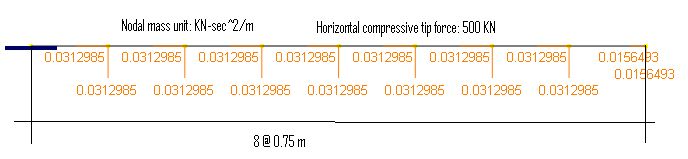
▪Generate the beam geometry by Create > Templates > Rectangular Frames.  For example, to generate 8 members (each with 0.75 m), enter a distance list of “8@0.75” in the X direction.  Do not enter anything for the Y and Z directions.

▪Select all members, define and assign the material properties by Modify > Member Properties > Materials. Make sure “Assign active material to currently selected elements” is checked in the dialog box.

▪Select all members, define and assign the section properties by Modify > Member Properties > Sections.  Make sure “Assign active section to currently selected members” is checked in the dialog box.

▪Press ESC key to unselect all nodes and elements.  Select the first node by Create > Select > Select Nodes, and assign it a fixed support by Create > Boundary Conditions > Support.

▪Apply self weight by running Create > Draw Loads > Self Weights.  Set self weight direction to be global Y and self weight multiplier -1.

▪Set the analysis options by Analysis > Analysis Options.  Choose the model type “2D Frame”.  Uncheck “Consider shear deformation on members”.  

▪From Analysis > Frequency Analysis, check “Convert loads to masses”, set number of modes 3, number of iteration vectors 8, tolerance of eigenvalue 1e-6 and maximum number of subspace iterations 18.

 

For Case a), do the following steps

▪Run Frequency Analysis from Analysis > Frequency Analysis

 

For Case b) do the following steps

▪From Tables > Masses > Calculated Masses, click on “Convert to Additional Masses”.  This is to avoid converting the external load to mass (although it is not necessary in this case because the load is not in the gravity direction).

▪Select the last node by Create > Select > Nodes, and assign it a nodal load of -500 KN in the global X direction.

▪From Create > Load Combinations, set the default load combination to “Perform P-Delta Analysis on this load combination”.

▪From Analysis > Frequency Analysis, make sure “Convert loads to masses” is unchecked.  Then click on Run Frequency Analysis.

 

Results

The frequencies without considering axial load can be calculated based with the following formulae [Ref. 14]:

and

where m is the linear mass density

m = 7850 * 53.1612 = 41.731542 kg/m

I = 4.07907 10-5 m^4

L = 6 m

E = 2.06 10-11 N/m^2

; ;

 

There are no closed form formulae for calculating frequencies when axial load influence is considered.  The results are therefore compared with another finite element program, AxisVM 6.0

 

The following table shows the first three frequencies modeled with 8 elements.  The comparison between the program and theoretical results is excellent.  The comparison between the program and AxisVM 6.0 is identical.

 

 

Comments

The comparison between the program and theoretical results is deemed excellent because we used only 8 elements for the discretization.  The frequencies given by the program are lower than the exact ones.  Notice the mass allocated to the support is lost in the computation.  If we employed more elements, the finite element frequencies would definitely be closer to the exact continuous ones.

 

When axial load is considered, as in Case b, the stress-stiffness concept used by ENERCALC 3D to determine P-Delta effects is applied.  In this approach, compressive axial load effectively reduces the flexural stiffness of a member (axial tension increases the flexural stiffness).  With a lower stiffness, and equal mass, the frequencies are reduced.