Navigation:  Dynamic > F-05 (Cantilever Brick Vibration)

Objective

To verify the behavior of brick element vibration

 

Problem Description

A 1.0 m long cantilever beam fixed at the left end as shown below vibrates under its own weight.  

 

Material properties: E = 2.0e11 N/m2, ν = 0, density = 7800 kg/m3

 

Beam section: b x h = 0.05 x 0.1 m

 

 

Finite Element Model

40 brick elements (20 x 2 x 1 mesh)

Model type: 3D Brick

Boundary conditions

Fixed Dx, Dy and Dz for nodes at left end

Fixed Dx for nodes along the middle line

Fixed Dz for all nodes

 

Results

The theoretical mode frequencies may be calculated as follows [Ref 1]:

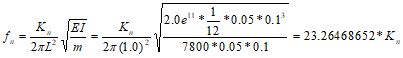
Where K1 = 3.51602; K2 = 22.0345; K3 = 61.6972

Unit: mode frequency – Hz

 

 

Comments

The first and second vibration frequencies given by ENERCALC 3D are close to the theoretical ones.  More elements need to be used to get accurate third and higher frequencies.

The boundary conditions are chosen such that out-of-plane and axial directions are suppressed so we can concentrate on the behavior of in-plane vibration.

 

Reference

[1]. Chopra, “Dynamics of Structures” 2nd Edition, pp 679, Prentice Hall, Inc., 2001