Navigation:  Static - Shell Element (Bending) > B-02 (Parapet)

Objective

To verify the plate (Kirchhoff thin plate formulation) element under constant twist.

 

Problem Description

A plate of size 240 x 240 in is subjected to a transverse point load of -10,000 lb at a corner D as shown below.  The boundary lines AB and AC are simply supported.

 

Material properties: E = 2.9e+007 psi, ν = 0.30

 

Thickness t = 10 in

 

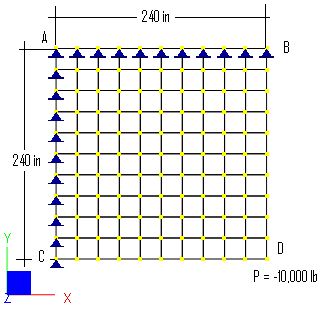
Finite Element Model

100 shell elements

Model type: 2D Plate Bending (Kirchhoff thin plate formulation)

 

Results

The displacements, internal forces, and moments may be calculated as follows [Ref 1]:

;

lb-in/in

in

 

Units: displacement – in; moment – lb-in/in

 

Comments

The results given by ENERCALC 3D are identical to the theoretical values.

This is an interesting problem which has practical applications (such as parapet at the corner of a building).  It shows that a plate structure may have pure twist Mxy (Mxx = Myy = 0).  Generally, for a homogeneous material such as steel, the strength should be checked based on principal stresses.  For a non-homogeneous material such as concrete, the strength should be checked based on principal moments (not just Mxx and Myy). In this example, reinforcement should be placed as shown below.  The solid lines represent the top reinforcement while the dashed lines do the bottom reinforcement.

 

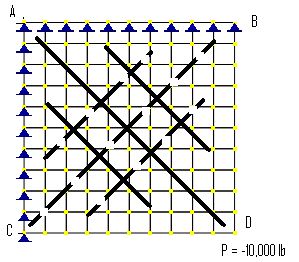
In practical applications for concrete slabs, reinforcement placed based on principal moments will be difficult.  Alternative methods are available.  One of these methods is the so-called Wood-Armer method [Ref 2].  It takes into account Mxy as well as Mxx and Myy for calculating top and bottom reinforcement in two orthogonal directions x and y.

 

Reference

[1]. Z.L Xu, “Elastic Mechanics” 3rd Ed., pp58, High Education Publishing House, China 1994

ISBN 7-04-002893-X/TB.159

[2]. Park & Gamble “Reinforced Concrete Slab”, pp202, John Wiley & Sons, Inc., 1980