Determining a suitable mesh density is more of an art than a science. There are no hard and fast rules to apply here, only general guidelines. The important thing to understand is that deflections are only reported at node locations, and shell stresses are only accurately reported at shell centers. So it is important to have nodes and shell centers relatively close to the locations of interest.
Mesh density becomes a tradeoff between having too few results locations and having too many results locations.
It helps to understand what happens at the extremes; that is when meshes are way too coarse and when meshes are way finer than they need to be.
Extremely coarse meshes will run more quickly than fine meshes, because of the significant reduction in the number of required calculations. But this can come at a cost of accuracy. For example, if a beam is known to have reverse curvature, we would never be able to sketch a reasonable guess for the deflected shape if we only had data for the endpoints and for one or two interior points. By sketching an assumed deflected shape and observing maxima, minima and points of inflection, you can start to establish a bare minimum number of data points that would be desirable for sketching a deflected shape. It stands to reason that you probably wouldn't want to create a mesh that is any more coarse than this, or it might not be useful in terms of quantifying the extremes.
On the other hand, extremely fine meshes will result in long run times and will produce reams and reams of data that may be difficult to sort through. There is also a risk of inaccuracies when meshes are excessively fine.
So the key is to balance the need for accurate results with the time it takes to process and the complexity of the output. Fortunately modern computers are extremely powerful and current finite element formulations are very efficient, so run times for average models may not be a big problem. And thanks for the sorting and postprocessing features in ENERCALC 3D, the process of reviewing reams of data is often reduced to a trivial task through efficient reporting and onscreen display tools. So when determining an adequate mesh density, it is generally advisable to err to the side of making it finer than it needs to be, rather than using a mesh that is too coarse.
For those who are not yet comfortable with establishing a suitable mesh density, here is a suggested procedure for helping to calibrate your judgment. Create a mesh that is obviously too coarse, and apply realistic loads so that analysis results can be obtained. Make note of some result of interest, such as the deflection or moment at a particular location. Modify the mesh density by making it more dense, and observe the effect in the result of interest. Then keep repeating the process until a break point is reached where further subdivision of the mesh no longer produces a change in the value of interest. This will ultimately lead to a mesh density that is optimized for the current conditions.
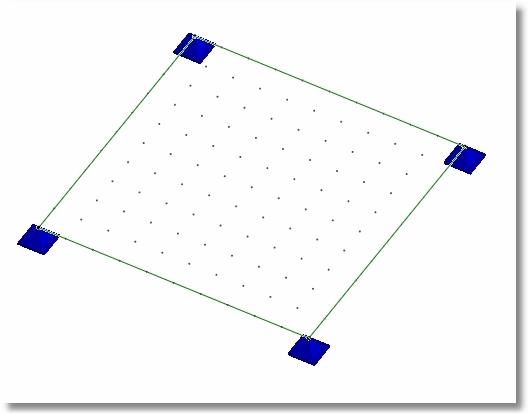
Mesh too coarse.

Mesh still too coarse.

Mesh getting better.
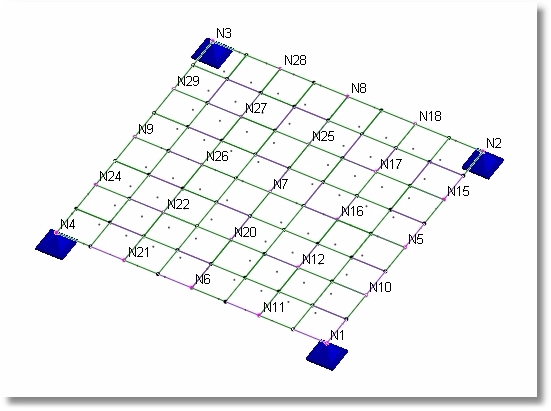
Mesh getting much better.
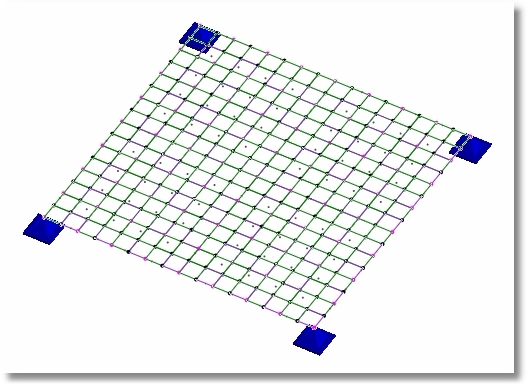
Could be ideal.
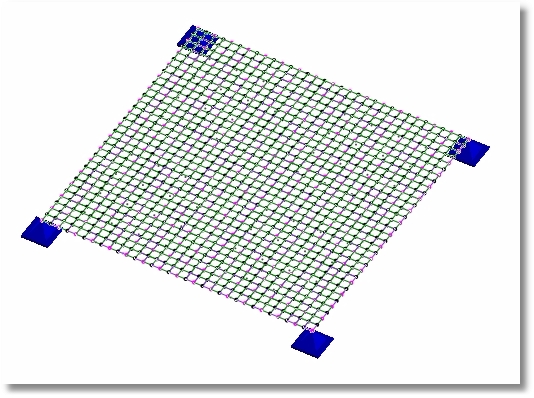
Probably finer mesh than necessary.

Mesh much too fine.