Step-By-Step Examples > Example 15: Design of Concrete Slab

Problem Description

The following 34 x 34 ft flat plate is supported by two fixed edges and two simply supported edges as well as a 16 x 16 in column in the middle. [Ref 20, pp 536-540].

Example 15 Design of Concrete Slab1

Factored load = 170 psf (including self-weight)

fc = 4 ksi, fy = 60 ksi

Slab thickness h = 6.5 in

Concrete cover: d = 1.25 in over the central column and near the intersection of the two fixed edges, d = 1.0 in for the rest of the area.

Suggested Modeling Steps

▪Set proper units from Settings and Tools > Units & Precisions. In particular, set the length unit to be inch for easy mesh generation.

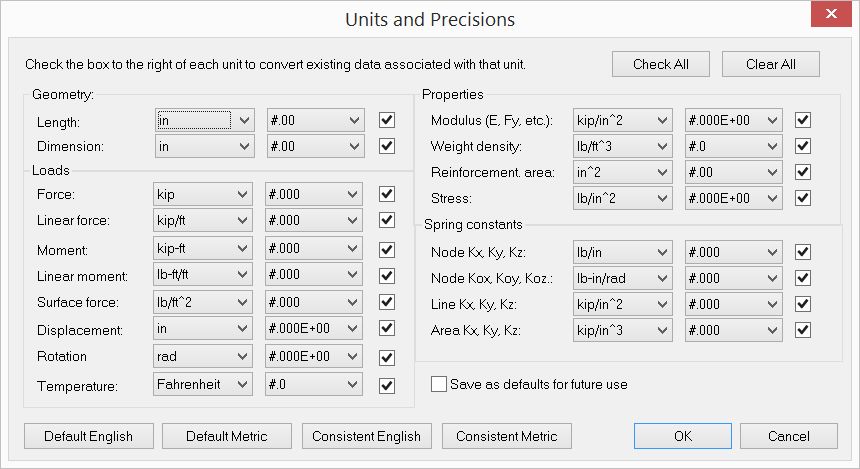
Example 15 Design of Concrete Slab2

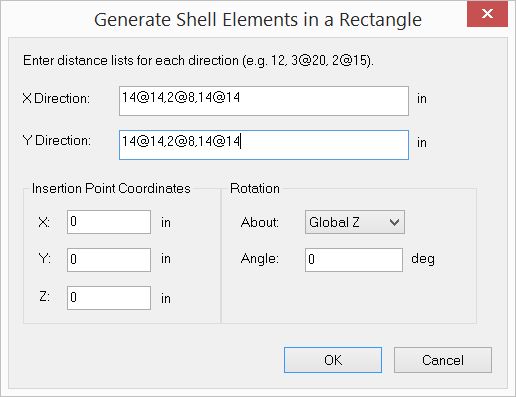
▪Generate rectangular shells by Create > Templates > Rectangular Shells as follows:

Example 15 Design of Concrete Slab3

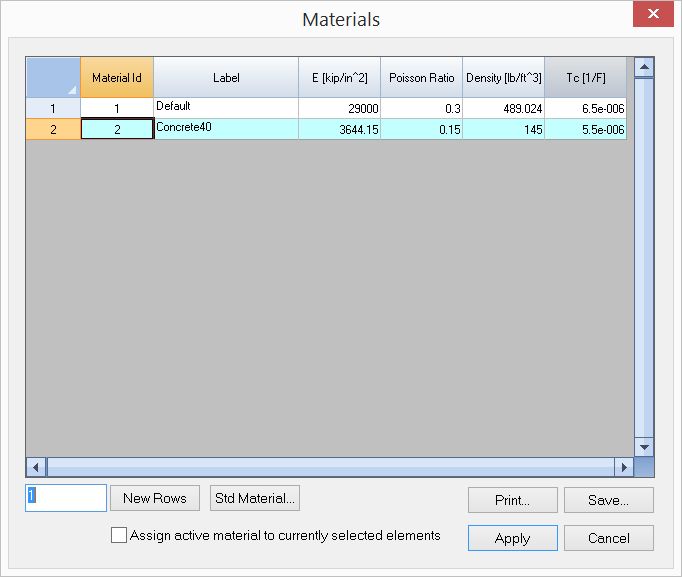
▪Define 4.0 ksi concrete material using Std Material in Modify > Shell Properties > Materials. Assign this material to all plates.

Example 15 Design of Concrete Slab4

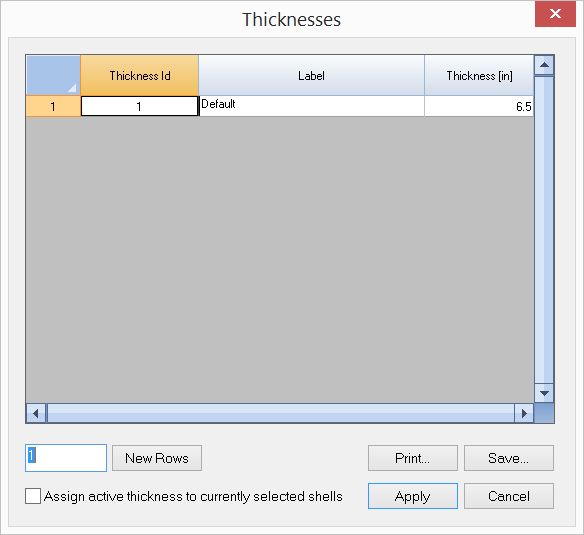
▪Define a thicknesses of 6 inches using Modify > Shell Properties > Thicknesses. Assign this thickness to all plates.

Example 15 Design of Concrete Slab5

▪Using Create > Boundary Conditions > Support, assign fixed supports to nodes along the left and bottom edges. Assign pinned supports to nodes along the right and top edges as well as to the column node.

▪Assign normal surface load of 170 lb/ft^2 to all plates by Create > Draw Loads > Surface Loads.

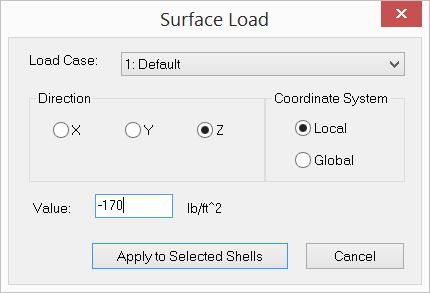
Example 15 Design of Concrete Slab6

▪You may turn off the display of surface loads by View > Load Diagram.

Example 15 Design of Concrete Slab7

▪Use the default load combination for concrete design from Create > Load Combinations.

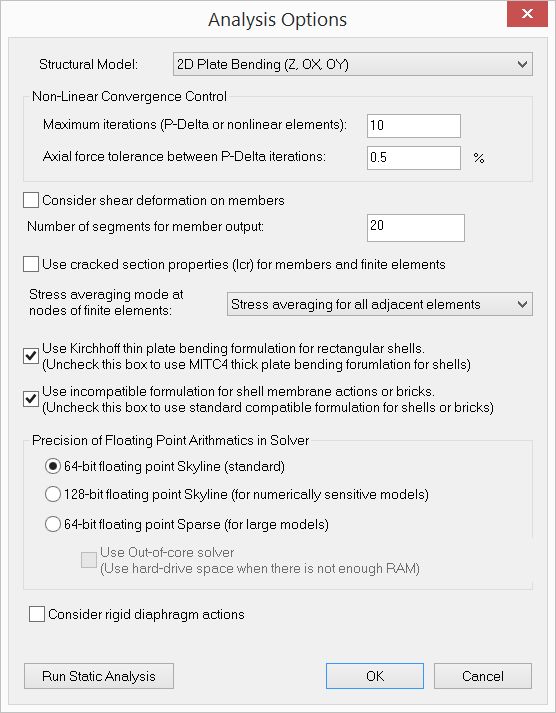
▪Set the analysis options by Analysis > Analysis Options. Choose the model type “2D Plate Bending”. Uncheck “Consider shear deformation on members”. Check “Use Kirchhoff thin plate bending formulation for rectangular shells”. The Kirchhoff element formulation is recommended over the MITC4 bending formulation for thin plate models that contain only rectangular elements. Run Static Analysis to make sure the model is correct before we proceed to the concrete design.

Example 15 Design of Concrete Slab8

▪Various analysis results may be viewed by Analysis Results > Contour Diagram. The following are Dz displacement, plate Mxx and Mxy contours.

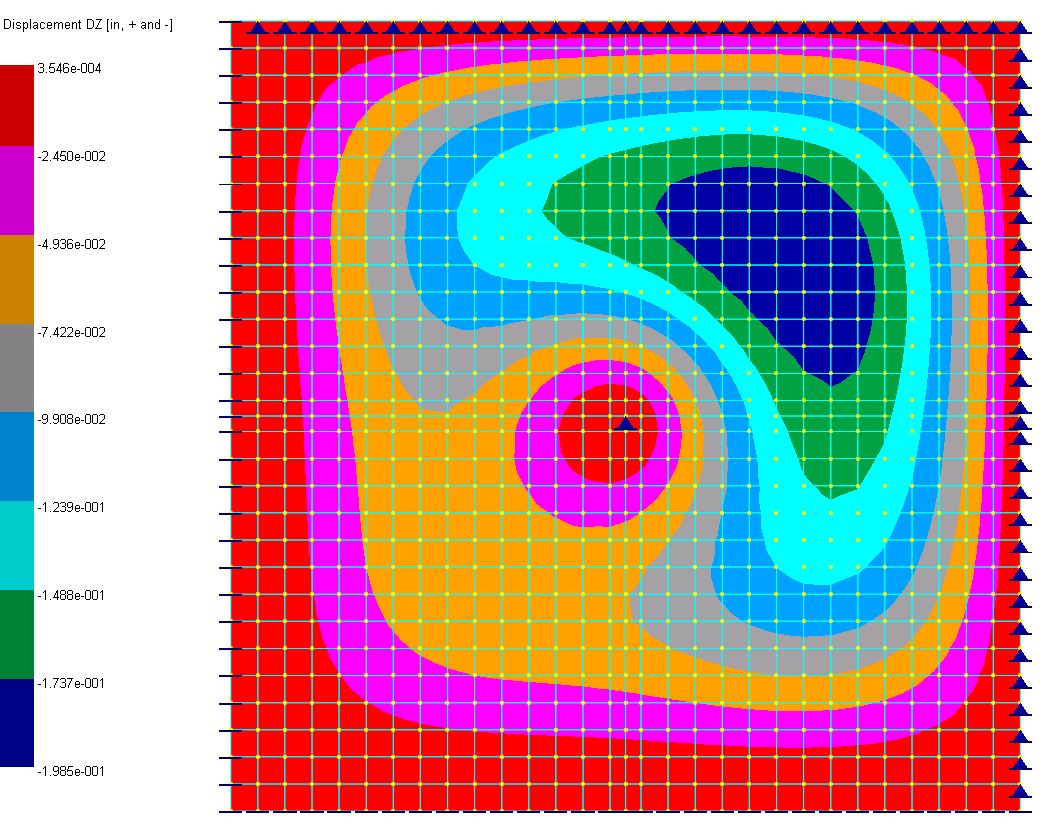
Example 15 Design of Concrete Slab9

Dz Displacement Contour

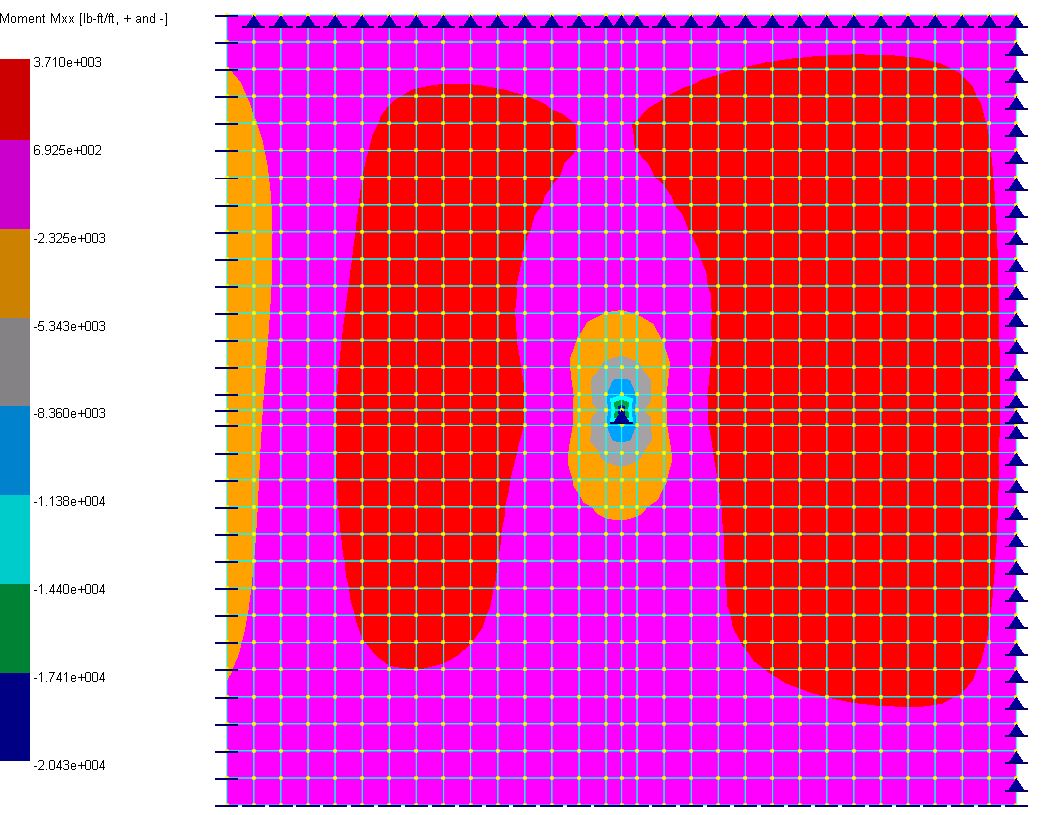
Example 15 Design of Concrete Slab10

Plate Mxx Contour

Example 15 Design of Concrete Slab11

Plate Mxy Contour

▪Select ASTM_615 (English) rebar database by Concrete Design > Concrete Design Tools > Rebar Database.

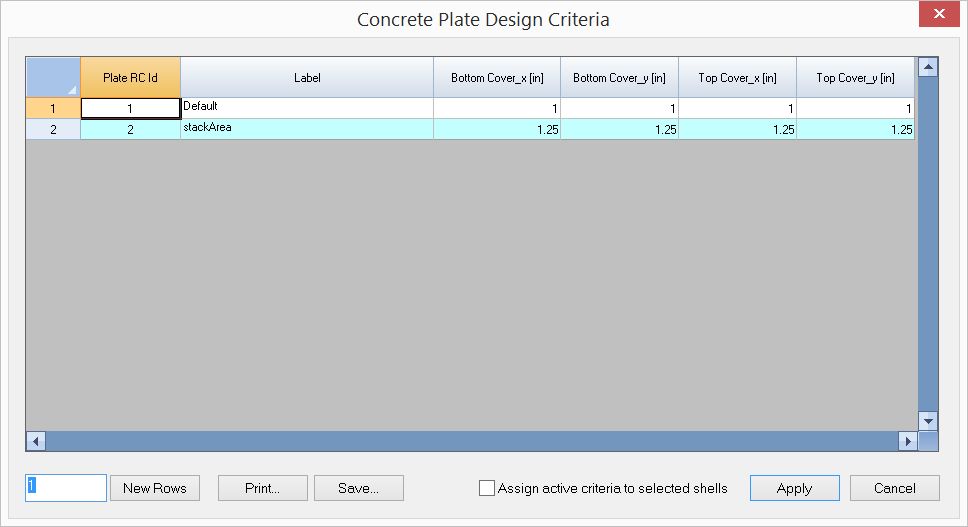
▪Define two plate design criteria by Concrete Design > RC Design Criteria > RC Plate Design Criteria as follows. Assign the stackArea criteria to area where bar stacking occurs – that is, over the central column and near the intersection of the two fixed edges.

Example 15 Design of Concrete Slab12

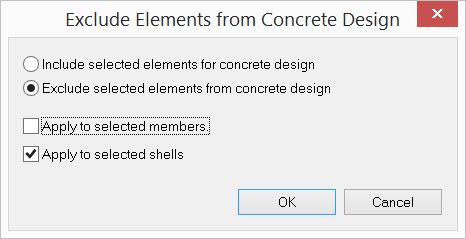
▪Select the four plates over the column node and exclude these plates from concrete design by Concrete Design > Exclude Elements.

Example 15 Design of Concrete Slab13

▪Perform concrete design by Concrete Design > Perform Concrete Design.

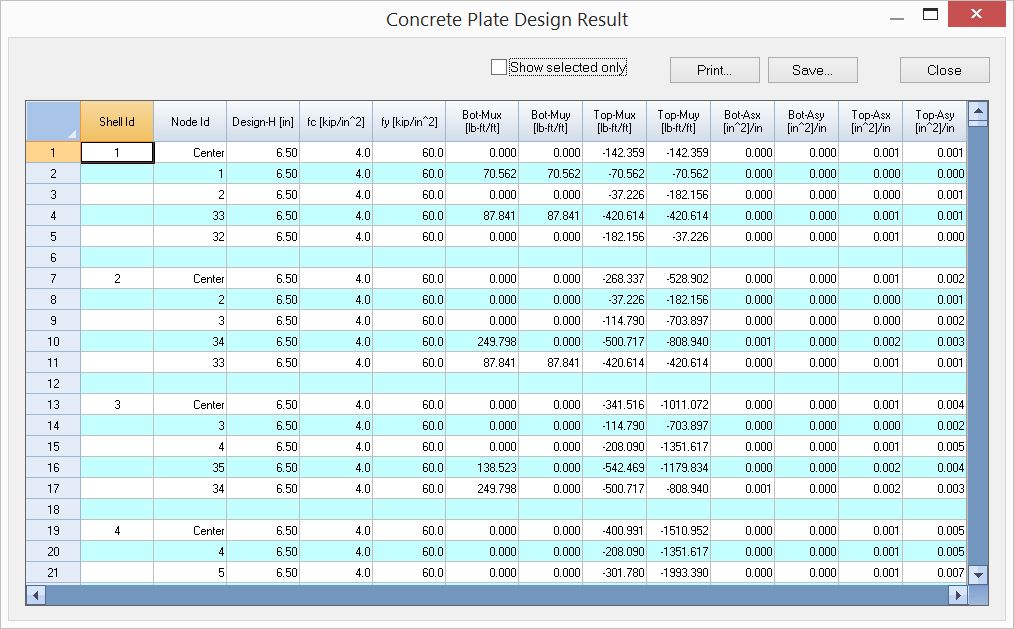
▪To view the plate flexural design results in tabulated form, run Concrete Design > Concrete Design Output > RC Plate Results.

Example 15 Design of Concrete Slab14

▪To view the plate design result in graphics, run Concrete Design > Concrete Design Diagrams > RC Plate Envelope Contour. For illustration purposes, the X-top and X-bottom design (Wood-Armer) moment and the corresponding required steel contours are shown below. Based on reinforcement contours and some common sense, the actual reinforcement can be provided for final design.

Example 15 Design of Concrete Slab15

Wood-Armer Top-Mux

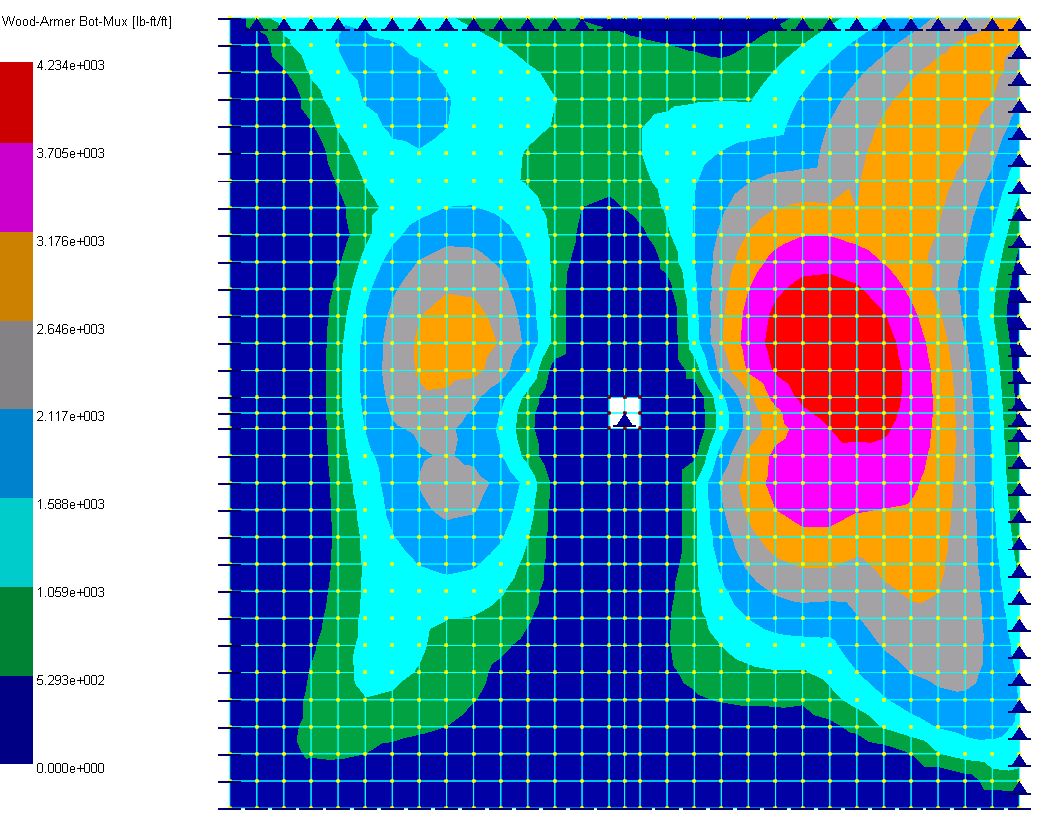
Example 15 Design of Concrete Slab16

Wood-Armer Bottom-Mux

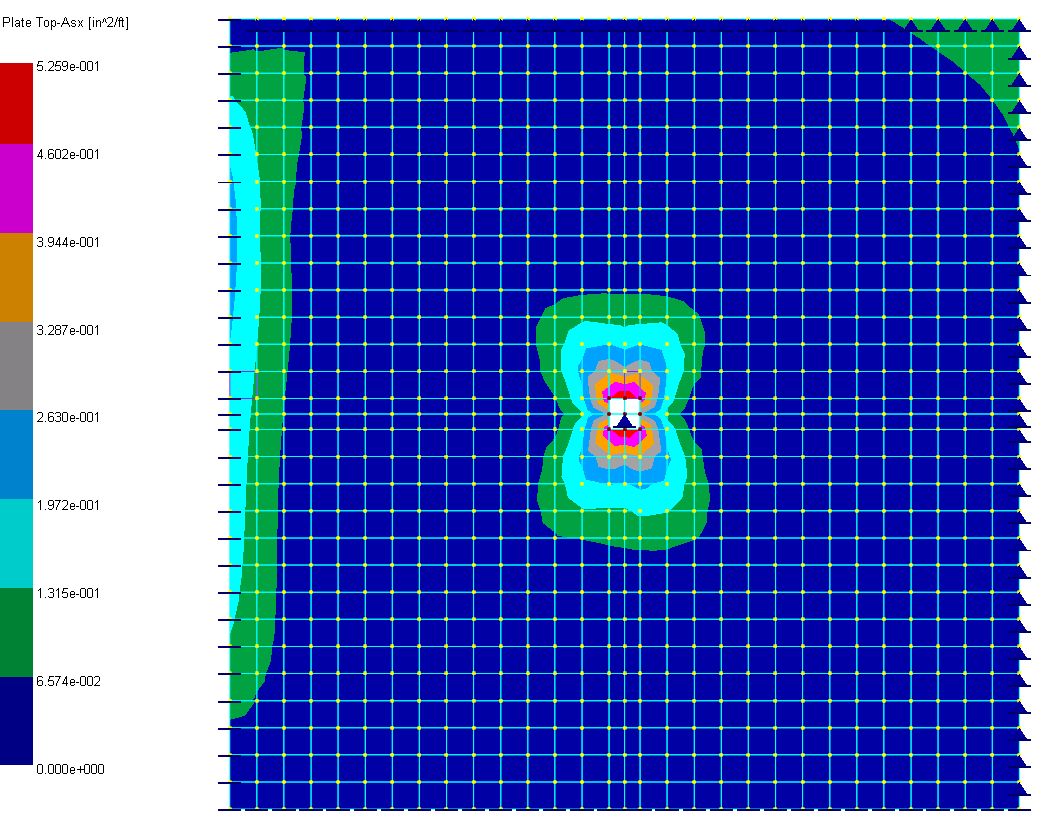
Example 15 Design of Concrete Slab17

Required Top-Asx

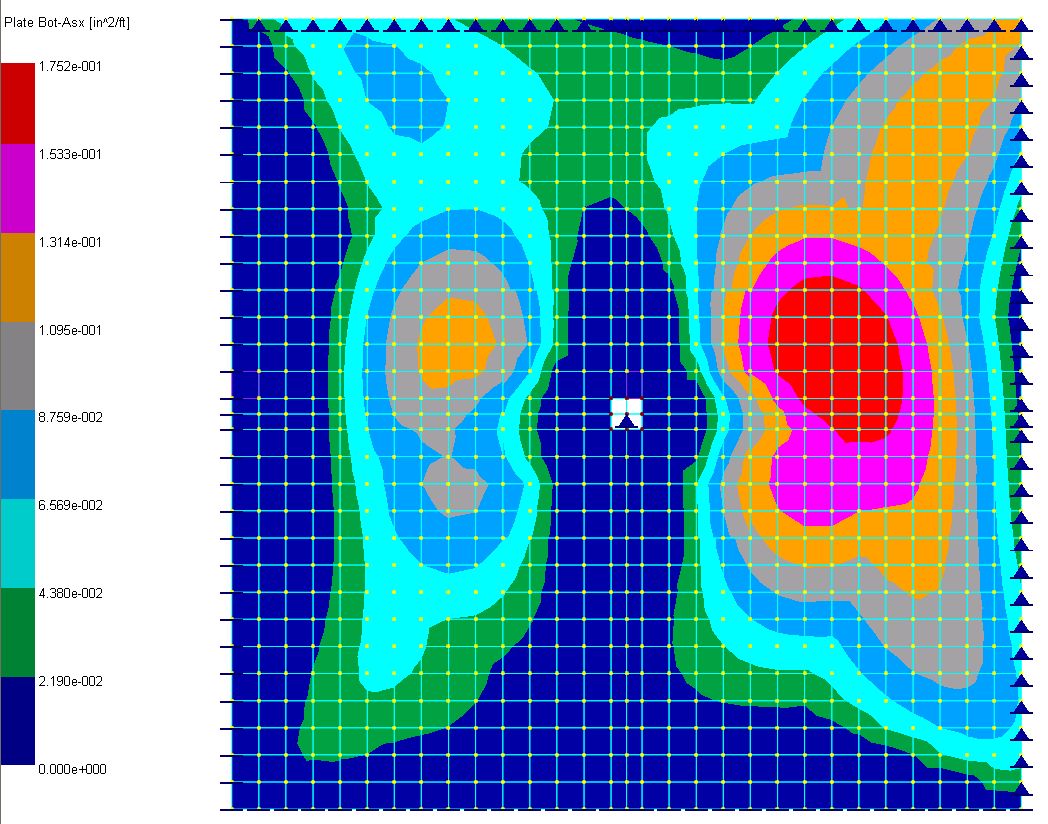
Example 15 Design of Concrete Slab18

Required Bottom-Asx

Results

	ENERCALC 3D	Ref 20
Negative moment over column (lb-ft/ft)	-11,510	-10,528
Negative steel over column (in^2/ft)	0.5259	0.48
Negative moment along fixed edges (lb-ft/ft)	-4,412	-3,509
Negative steel along the fixed edges (in^2/ft)	0.183	0.15
Positive moment in outer spans (lb-ft/ft)	4,234	3,789
Positive steel in outer spans (in^2/ft)	0.1752	0.16

Comments

The reference used Advanced Strip Method to compute the design moments and therefore is approximate in nature. The program computes the design (Wood-Armer) moments based on the plate element Mxx, Myy and Mxy. Although the two methods are fundamentally different, comparable results are obtained.

One of the difficulties in using finite element results to perform concrete plate (or slab) design is stress singularity. In this example, the slab stress around the column is theoretically infinite. This is reflected in stress and reinforcement spikes at the slab/column interface area. Finer finite element mesh will generally exacerbate the problem. We alleviated the problem by excluding the four finite elements over the column from design. Appropriate averaging or redistribution of reinforcement should also be applied before the actual reinforcement is provided.