C-01 (Membrane Patch Test) |
  
|
C-01 (Membrane Patch Test) |
|
Objective
To verify membrane formulations pass the patch test
Problem Description
A plate of size 0.24 x 0.12 in is subjected to forced displacements at the four corners as shown below. The boundary conditions are: u = 10-3(x + y / 2); v = 10-3(y + x / 2)
Material properties: E = 1.0e6 psi, ν = 0.25
Geometry: nodal coordinates are shown in the parenthesis below, thickness t = 0.001 in
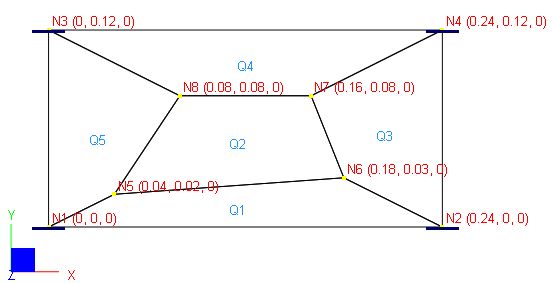
Finite Element Model
5 shell elements
Model type: 2D Plane Stress
Forced displacements on boundary nodes:
Unit: displacement - in
Boundary Nodes |
Displacement Dx |
Displacement Dy |
1 |
0 |
0 |
2 |
2.4e-4 |
1.2e-4 |
3 |
6.0e-5 |
1.2e-4 |
4 |
3.0e-4 |
2.4e-4 |
Results
The displacements of internal nodes can be calculated based on the boundary conditions. The constant strains may be calculated as follows:
; 
;
Constant stresses may be calculated accordingly and are given in [Ref 1].
Unit: displacement - in
Internal Node |
ENERCALC 3D |
Theoretical |
||
Displacement Dx |
Displacement Dy |
Displacement Dx |
Displacement Dy |
|
5 |
5.00e-5 |
4.00e-5 |
5.00e-5 |
4.00e-5 |
6 |
1.95e-4 |
1.20e-4 |
1.95e-4 |
1.20e-4 |
7 |
2.00e-4 |
1.60e-4 |
2.00e-4 |
1.60e-4 |
8 |
1.20e-4 |
1.20e-4 |
1.20e-4 |
1.20e-4 |
Unit: stress - psi
ENERCALC 3D |
[Ref 1] |
||||
Stress Sxx |
Stress Syy |
Stress Sxy |
Stress Sxx |
Stress Syy |
Stress Sxy |
1333 |
1333 |
400 |
1333 |
1333 |
400 |
Comments
The results given by ENERCALC 3D are identical to the theoretical and referenced values.
A patch test consists of creating a small “patch” of elements and then imposing an assumed displacement field at the boundary nodes. The assumed displacement field is chosen such that it causes a constant stress in the mesh. To pass the patch test, computed displacements at the interior nodes must be consistent with the assumed displacement field and the computed stresses must be constant. Patch tests are important because they ensure solution convergence—so that increasing mesh fineness results in more accurate results.
Both compatible and incompatible membrane formulations pass the patch test.
Reference
[1]. MacNeal & Harder, “A Proposed Standard Set of Problems to Test Finite Element Accuracy”, Finite Elements in Analysis and Design, 1 (1985) 3-20
[2]. Cook, Malkus, Plesha, Witt, “Concept and Applications of Finite Element Analysis” 4th Edition, pp238, John Wiley & Sons, Inc., 2002
