Static - Shell Element (Bending) > B-04 (Fixed Rectangle)

Objective

To verify the behavior of the MTC4 thick plate and the Kirchhoff thin plate bending elements

Problem Description

A 3.2 x 2 in rectangular plate is fixed on all edges and subjected to a uniform pressure of q = -1e-4 psi as shown below.

Material properties: E = 1.7472e7 psi, ν = 0.3

Thickness: t = 1e-4 in

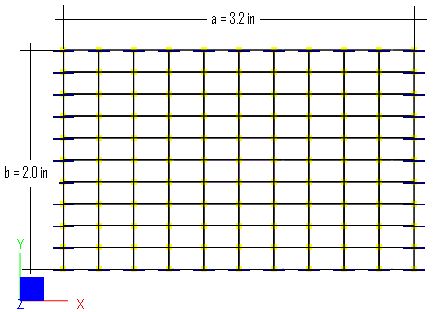
B-04 (Fixed Rectangle)1

Finite Element Model

100 shell elements

Model type: 2D Plate Bending (MITC4 thick plate and Kirchhoff thin plate)

Results

The displacements and stresses are compared with those produced by another program, ADINA. Theoretical results are calculated as follows [Ref 1]:

Displacement @ center: in

Stress @ center of long edge: psi

Stress @ center: psi

Units: displacement – in; rotation – rad; stress - psi

	ENERCALC 3D		ADINA	Theoretical
	MITC4 (thick)	Kirchhoff (thin)	ADINA	Theoretical
Displacement Dz @ center	-2.274	-2.342	-2.274	2.299
Max Rotation Dox	3.653	3.608	3.653	-
Max Rotation Doy	2.502	2.373	2.502	-
Stress Sxx @ center of short edge	7507	12927	7507	-
Stress Sxx @ center	-4880	-4763	-4880	-
Stress Syy @ center of long edge	13478	18743	13478	18720
Stress Syy @ center	-9143	-9483	-9143	-9144
Max Stress Sxy	2556	2459	2556	-

Comments

The results given by ENERCALC 3D using the MITC4 are identical to those given by another reputable finite element program, ADINA. The results also compare well with the theoretical results based on the thin plate theory. The stress prediction of the MITC4 thick plate at the boundary seems to be less accurate than that of the Kirchhoff thin plate.

The following illustrates displacement and stress contours (not smoothed) based on the MITC4 thick plate.

B-04 (Fixed Rectangle)5