Static - Beam Element > A-13 (2D Truss with an Inclined Roller)

Objective

To verify the behavior of inclined roller using multi-DOF constraint

Problem Description

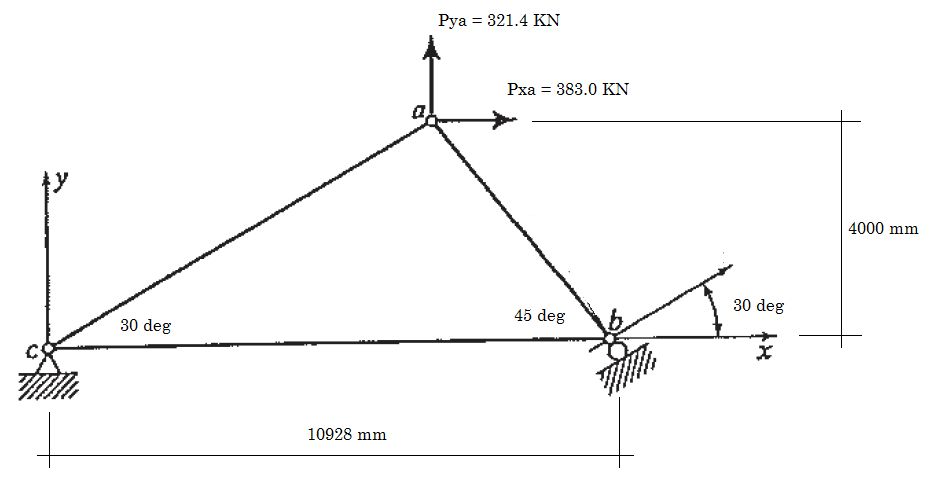
A truss [Ref 1] is supported by a pinned support at point c and a roller (inclined at 30 degrees from horizontal line) at point b as shown below.

Sections: ab = 20,000 mm^2, ac = 15,000 mm^2, bc = 18,000 mm^2

Material: E = 200 MPa

A-13 (2D Truss with an Inclined Roller)1

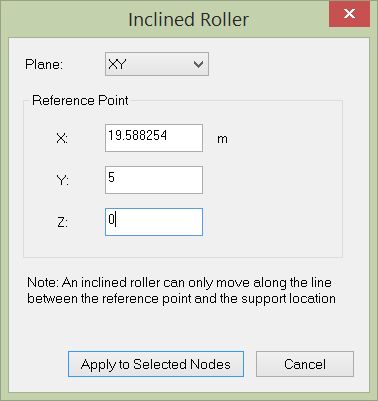
When creating the inclined roller, we can set any point along the roller angle line as the reference point. For example, if the coordinate at point b is (10.928, 0, 0), then we can set the reference point as (10.928 + 10 * cos30, 10 * sin30, 0) = (19.588254, 5, 0).

A-13 (2D Truss with an Inclined Roller)2

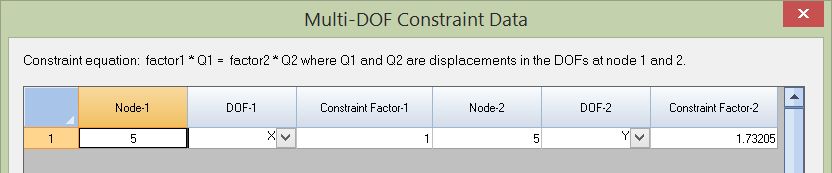
This effectively creates a multi-DOF constraint as the following:

A-13 (2D Truss with an Inclined Roller)3

Results

The following are the displacements and support reactions given by ENERCALC 3D and [Ref 1]. The reaction resultant @ b is calculated by hand as following: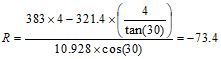 A-13 (2D Truss with an Inclined Roller)4 kN (pointing to bottom-right).kNkN

	ENERCALC 3D	Ref 1
Displacement Dx @ a	0.9282 mm	0.928 mm
Displacement Dy @ a	1.142 mm	1.143 mm
sqrt(Dx * Dx + Dy * Dy) @ b	0.09416 mm	0.094 mm
Reaction Rx @ c	-419.70 kN	-419.7 kN (by hand)
Reaction Ry @ c	-257.83 kN	-257.83 kN (by hand)
Reaction Rx @ b	36.70 kN (constrained force)	36.70 kN (by hand)
Reaction Ry @ b	-63.57 kN (constrained force)	-63.57 kN (by hand)

Comments

The displacement results given by ENERCALC 3D are very close to the referenced values. The support reactions are not given in Ref 1 but can be easily calculated by hand, which match exactly with those given by ENERCALC 3D.

Reference

[1]. W. McGuire & R.H. Gallagher & R.D. Ziemian, “Matrix Structural Analysis” pp 390, 2nd ed., John Wiley & Sons, Inc., 2000