Static - Beam Element > A-11 (2D Frame with Support Settlements)

Objective

To verify the behavior of the forced translational and rotational displacements

Problem Description

A frame [Ref 1] is clamped at point A and rolled at points B and C as shown below. The relative flexural stiffness of each element is shown in a circle. No external load is applied to the frame, but the frame is subjected to settlement of fixed support A. Assume that the vertical, horizontal, and angular settlements are a = 2 cm, b = 1 cm, and ᵩ = 0.01 rad, respectively.

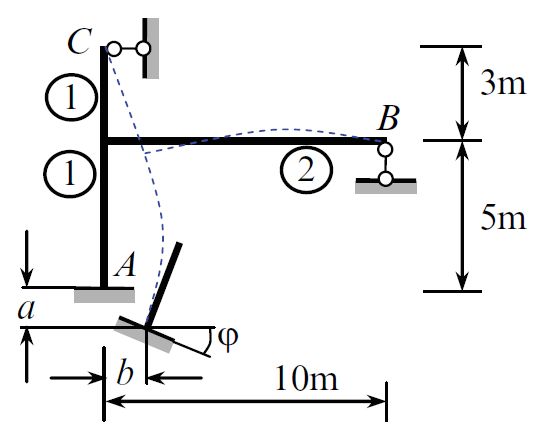
A-11 (2D Frame with Support Settlements)1

Finite Element Model

Model type: 2D Frame, without considering frame shear deformation.

The reference does not specify material and section specifically, so we will use steel and rectangular sections (100 mm x 100 mm for vertical members and 200 mm x 100 mm for horizontal member, which satisfy the relative flexural stiffness of members).

E = 200 kN/mm2, I = 8.33333e+006 mm4

Results

The support reactions given by ENERCALC 3D are shown below.

	ENERCALC 3D	Ref 1
Reaction Moz @ A	7.57 kN-m	C1 * EI = 4.5418 * 10-3 * (1/m) * 200 kN/mm2 * 8.333 * 106 mm4 = 7.5667 kN-m
Reaction Ry @ B	-0.19 kN	C2 * EI = -1.119 * 10-4 * m2 * 200 kN/mm2 * 8.333 * 106 mm4 = -0.1865 kN
Reaction Rx @ C	-1.18 kN	C3 * EI = -7.076 * 10-4 * m2 * 200 kN/mm2 * 8.333 * 106 mm4 = -1.179 kN

Note: From [Ref 1]

C1 = 4.5418 * 10-3 (unit: 1/m)

C2 = -1.119 * 10-4 (unit: 1/m2)

C3 = -7.076 * 10-4 (unit: 1/m2)

Comments

The results given by ENERCALC 3D are very close to the referenced values.

Reference

[1]. Igor A. Karnovsky, Olga Lebed, “Advanced Methods of Structural Analysis”, pp 248, Springer Science+Business Media, LLC, 2010.